В большинстве учебников алгебры эта теорема формулируется для приведенного квадратного уравнения и гласит, что если уравнение 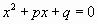 имеет корни
имеет корни 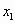 и
и 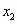 , то для них выполняются равенства
, то для них выполняются равенства 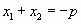 ,
, 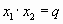 . Затем формулируется утверждение, обратное к теореме Виета, и предлагается ряд примеров для отработки этой темы.
. Затем формулируется утверждение, обратное к теореме Виета, и предлагается ряд примеров для отработки этой темы.
Возьмем конкретные примеры и проследим на них логику решения с помощью теоремы Виета.
Выделим основные этапы рассуждений при решении приведенного квадратного уравнения 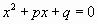 с помощью теоремы Виета:
с помощью теоремы Виета:
| записать утверждение теоремы Виета | 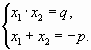 | (*) |
(первым равенством рекомендуется записывать произведение корней);
- определить знаки корней уравнения (Если произведение и сумма корней – положительные, то оба корня – положительные числа. Если произведение корней – положительное число, а сумма корней – отрицательное, то оба корня – отрицательные числа. Если произведение корней – отрицательное число, то корни имеют разные знаки. При этом, если сумма корней – положительная, то больший по модулю корень является положительным числом, а если сумма корней меньше нуля, то больший по модулю корень – отрицательное число);
- подобрать пары целых чисел, произведение которых дает верное первое равенство в записи (*);
- из найденных пар чисел выбрать ту пару, которая при подстановке во второе равенство в записи (*) даст верное равенство;
- указать в ответе найденные корни уравнения.
Заметим, что теорему Виета в принципе можно сформулировать и для полного квадратного уравнения: если квадратное уравнение 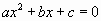 имеет корни
имеет корни 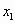 и
и 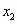 , то для них выполняются равенства
, то для них выполняются равенства 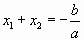 ,
, 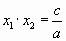 . Однако применение этой теоремы довольно проблематично, так как в полном квадратном уравнении по крайней мере один из корней (при их наличии, конечно) является дробным числом. А работать с подбором дробей долго и трудно. Но все-таки выход есть.
. Однако применение этой теоремы довольно проблематично, так как в полном квадратном уравнении по крайней мере один из корней (при их наличии, конечно) является дробным числом. А работать с подбором дробей долго и трудно. Но все-таки выход есть.
Рассмотрим полное квадратное уравнение 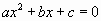 . Умножим обе части уравнения на первый коэффициент а и запишем уравнение в виде
. Умножим обе части уравнения на первый коэффициент а и запишем уравнение в виде 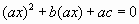 . Введем новую переменную
. Введем новую переменную 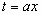 и получим приведенное квадратное уравнение
и получим приведенное квадратное уравнение 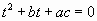 , корни которого
, корни которого 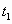 и
и 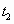 (при их наличии) могут быть найдены по теореме Виета. Тогда корни исходного уравнения будут
(при их наличии) могут быть найдены по теореме Виета. Тогда корни исходного уравнения будут 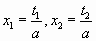 . Обратим внимание, что составить вспомогательное приведенное уравнение
. Обратим внимание, что составить вспомогательное приведенное уравнение 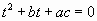 очень просто: второй коэффициент сохраняется, а третий коэффициент равен произведению ас. При определенном навыке учащиеся сразу составляют вспомогательное уравнение, находят его корни по теореме Виета и указывают корни заданного полного уравнения.
очень просто: второй коэффициент сохраняется, а третий коэффициент равен произведению ас. При определенном навыке учащиеся сразу составляют вспомогательное уравнение, находят его корни по теореме Виета и указывают корни заданного полного уравнения.
Решите уравнение 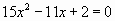 .
.
Решение
Составим вспомогательное уравнение 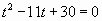 и по теореме Виета найдем его корни
и по теореме Виета найдем его корни 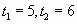 . А значит, корни исходного уравнения
. А значит, корни исходного уравнения 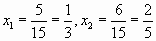 .
.
Ответ: 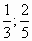 .
.
И еще один случай, когда применение теоремы Виета позволяет устно найти корни полного квадратного уравнения. Нетрудно доказать, что число 1 является корнем уравнения 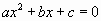 , тогда и только тогда, когда
, тогда и только тогда, когда 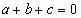 . Второй корень уравнения находится по теореме Виета и равен
. Второй корень уравнения находится по теореме Виета и равен 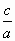 . Еще одно утверждение: чтобы число –1 являлось корнем уравнения
. Еще одно утверждение: чтобы число –1 являлось корнем уравнения 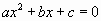 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 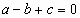 . Тогда второй корень уравнения по теореме Виета равен
. Тогда второй корень уравнения по теореме Виета равен 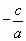 . Аналогичные утверждения можно сформулировать и для приведенного квадратного уравнения.
. Аналогичные утверждения можно сформулировать и для приведенного квадратного уравнения.
Решите уравнение 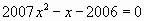 .
.
Решение
Заметим, что сумма коэффициентов уравнения равна нулю. Значит, корни уравнения 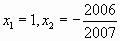 .
.
Ответ: 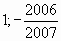 .
.
Решите уравнение 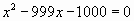 .
.
Решение
Для коэффициентов этого уравнения выполняется свойство 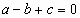 (действительно, 1-(-999)+(-1000)=0). Значит, корни уравнения
(действительно, 1-(-999)+(-1000)=0). Значит, корни уравнения 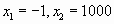 .
.
Ответ: .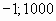 .
.
Использованы материалы http://festival.1september.ru/articles/503928/
Комментариев нет:
Отправить комментарий